Latent basis growth curve models in ABCD
References are linked throughout the text
Introduction
Using Latent Basis Growth Modelling (LBGM; Duncan & Duncan, 2009) we determined average trajectories of brain development based on fractional anisotropy (FA) data.
This script reproduces the latent basis growth model, which has been preregistered. We fitted four latent basis growth models across age 9 to 13 (split into five timepoints, e.g., one per year of age) to estimate trajectories of brain connectivity across four different brain regions. These regions included:
All brain tracts
Corpus callosum
Fornix
Anterior thalamic radiations
Packages used in this code include: tidyverse, ggplot2, readxl, lavaan, semPlot, tidyr, dplyr, semTools, regsem, quest, egg, ggpubr, extrafont
Latent basis growth curve models
A Latent Basis Growth Curve Model is a flexible growth model that allows for complex nonlinear patterns of change. An outcome measure is measured on several occasions, as we study changes over time. Random effects are used to capture individual differences. The random effects are represented by (continuous) latent variables, often called growth factors.
Before interpreting the data, make sure to first verify that the model fits the data. Reference here.
CFI and TLA should be .90 good model fit, now .95 is considered good
RMSEA: less than .05 = excellent, less than .08 = moderate/good, over .10 = poor fit
SRMR: less than .08 is good
All Tracts
Interpreting the results - Overall DTI
Chi-square test of overall model fit:
- The chi-square test (chisq = 17.937, p= 0.012), was statistically significant, therefore, this is an indication of a poor model fit.
Comparative Fit Index (CFI):
- Value is above 0.95 (CFI = 0.999), therefore, this indicates a good model fit.
Root mean square error of approximation (RMSEA):
- Value is less than 0.05 (RMSEA = 0.012), therefore, indicating a good model fit.
Interpreting the model
Variances
Intercept: initial status/baseline score
- Intercept (152.603, p=0.000)
Slope: change
- Slope (18.542, p =0.352)
Intercepts i:
Mean for the latent intercept, i, is 56.432, indicating that on average the DTI strength is around 56 at all time periods.
The intercept is significant, therefore indicating individual differences in baseline levels at age 9.
Intercepts s (represents the average rate of change for all the respondents):
Mean for the latent slope, s, is 7.183, indicating that on average DTI increased around 7 units between each time point.
There was no significant slope intercept, indicating that there are no significant growth trajectories.
Covariance:
- The covariance between the intercept and slope, -13.255, suggests that there is less DTI growth for those participants that had higher DTI scores at time point one than for those participants with lower DTI.
Residual variances (unexplained variance):
- The residual variances are between 13-22, indicating that each single-latent intercept model explained 78-87% of the variability in DTI score
m1 <- '
i =~ 1*t1_p1 + 1*t2_p1 +1*t3_p1 + 1*t4_p1 +1*t5_p1
s =~ 0*t1_p1 + t2_p1 + t3_p1 + t4_p1 + 1*t5_p1
'
fit_m1 <- growth(m1, data=POMPSGMMDTI, missing="fiml",estimator="mlr",bounds=TRUE,em.h1.iter.max= 10000)
fitMeasures(fit_m1,fit.measures=c("dfi","chisq","cfi","rmsea","srmr")) ## chisq cfi rmsea srmr
## 17.937 0.999 0.012 0.026summary(fit_m1, standardized=T, rsquare=T)## lavaan 0.6.16 ended normally after 183 iterations
##
## Estimator ML
## Optimization method NLMINB
## Number of model parameters 13
##
## Number of observations 10808
## Number of missing patterns 13
##
## Model Test User Model:
## Standard Scaled
## Test Statistic 17.937 11.401
## Degrees of freedom 7 7
## P-value (Chi-square) 0.012 0.122
## Scaling correction factor 1.573
## Yuan-Bentler correction (Mplus variant)
##
## Parameter Estimates:
##
## Standard errors Sandwich
## Information bread Observed
## Observed information based on Hessian
##
## Latent Variables:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## i =~
## t1_p1 1.000 12.353 0.941
## t2_p1 1.000 12.353 0.958
## t3_p1 1.000 12.353 0.958
## t4_p1 1.000 12.353 0.964
## t5_p1 1.000 12.353 0.983
## s =~
## t1_p1 0.000 0.000 0.000
## t2_p1 0.283 0.027 10.553 0.000 1.220 0.095
## t3_p1 0.523 0.024 21.682 0.000 2.251 0.175
## t4_p1 0.777 0.039 19.910 0.000 3.347 0.261
## t5_p1 1.000 4.306 0.343
##
## Covariances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## i ~~
## s -13.255 9.550 -1.388 0.165 -0.249 -0.249
##
## Intercepts:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## .t1_p1 0.000 0.000 0.000
## .t2_p1 0.000 0.000 0.000
## .t3_p1 0.000 0.000 0.000
## .t4_p1 0.000 0.000 0.000
## .t5_p1 0.000 0.000 0.000
## i 56.432 0.161 351.298 0.000 4.568 4.568
## s 7.183 0.308 23.326 0.000 1.668 1.668
##
## Variances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## .t1_p1 19.670 5.279 3.726 0.000 19.670 0.114
## .t2_p1 19.695 2.918 6.749 0.000 19.695 0.118
## .t3_p1 22.366 2.515 8.892 0.000 22.366 0.135
## .t4_p1 21.133 4.384 4.821 0.000 21.133 0.129
## .t5_p1 13.405 7.480 1.792 0.073 13.405 0.085
## i 152.603 6.163 24.760 0.000 1.000 1.000
## s 18.542 19.923 0.931 0.352 1.000 1.000
##
## R-Square:
## Estimate
## t1_p1 0.886
## t2_p1 0.882
## t3_p1 0.865
## t4_p1 0.871
## t5_p1 0.915semPaths(fit_m1)
Corpus Callosum
Interpreting the results - Corpus Callosum
Chi-square test of overall model fit:
- The chi-square test (chisq = 10.493, p= 0.162), was statistically significant, therefore, this is an indication of a poor model fit.
Comparative Fit Index (CFI):
- Value is above 0.95 (CFI = 1),therefore, indicating a good model fit.
Root mean square error of approximation (RMSEA):
- Value is less than 0.05 (RMSEA = 0.007), therefore, indicating a good model fit.
Interpreting the model
Variances:
Intercept (171.277, p=0.000)
Slope (30.953, p = 0.162)
Intercepts i:
- Mean for the latent intercept, i, is 62.143, indicating that on average the DTI strength is around 62 at all time periods.
Intercepts s:
- Mean for the latent slope, s, is 4.657, indicating that on average DTI increased around 4 units between each time point.
Covariance:
- The covariance between the intercept and slope, -20.747, suggests that there is less DTI growth for those participants that had higher DTI scores at time point one than for those participants with lower DTI.
Residual variances (unexplained variance):
- The residual variances are between 16-25, indicating that each single-latent intercept model explained 75-84% of the variability in DTI scores.
CCm1 <- '
i =~ 1*CCt1_p1 + 1*CCt2_p1 + 1*CCt3_p1 + 1*CCt4_p1 + 1*CCt5_p1
s =~ 0*CCt1_p1 + CCt2_p1 + CCt3_p1 + CCt4_p1 + 1*CCt5_p1
'
fit_CCm1 <- growth(CCm1, data=CCPOMPSGMMDTI, missing="fiml",estimator='mlr',bounds=TRUE,em.h1.iter.max= 10000)
fitMeasures(fit_CCm1,fit.measures=c("dfi","chisq","cfi","rmsea","srmr")) ## chisq cfi rmsea srmr
## 10.493 1.000 0.007 0.022summary(fit_CCm1, standardized=T, rsquare=T)## lavaan 0.6.16 ended normally after 237 iterations
##
## Estimator ML
## Optimization method NLMINB
## Number of model parameters 13
##
## Number of observations 10808
## Number of missing patterns 13
##
## Model Test User Model:
## Standard Scaled
## Test Statistic 10.493 5.966
## Degrees of freedom 7 7
## P-value (Chi-square) 0.162 0.544
## Scaling correction factor 1.759
## Yuan-Bentler correction (Mplus variant)
##
## Parameter Estimates:
##
## Standard errors Sandwich
## Information bread Observed
## Observed information based on Hessian
##
## Latent Variables:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## i =~
## CCt1_p1 1.000 13.087 0.956
## CCt2_p1 1.000 13.087 0.974
## CCt3_p1 1.000 13.087 0.966
## CCt4_p1 1.000 13.087 0.982
## CCt5_p1 1.000 13.087 1.003
## s =~
## CCt1_p1 0.000 0.000 0.000
## CCt2_p1 0.261 0.047 5.542 0.000 1.450 0.108
## CCt3_p1 0.516 0.039 13.123 0.000 2.869 0.212
## CCt4_p1 0.739 0.070 10.528 0.000 4.114 0.309
## CCt5_p1 1.000 5.564 0.426
##
## Covariances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## i ~~
## s -20.747 9.843 -2.108 0.035 -0.285 -0.285
##
## Intercepts:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## .CCt1_p1 0.000 0.000 0.000
## .CCt2_p1 0.000 0.000 0.000
## .CCt3_p1 0.000 0.000 0.000
## .CCt4_p1 0.000 0.000 0.000
## .CCt5_p1 0.000 0.000 0.000
## i 62.134 0.168 369.100 0.000 4.748 4.748
## s 4.657 0.332 14.014 0.000 0.837 0.837
##
## Variances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## .CCt1_p1 16.138 4.970 3.247 0.001 16.138 0.086
## .CCt2_p1 17.889 2.796 6.398 0.000 17.889 0.099
## .CCt3_p1 25.415 2.872 8.850 0.000 25.415 0.138
## .CCt4_p1 20.186 4.545 4.441 0.000 20.186 0.114
## .CCt5_p1 9.463 9.148 1.034 0.301 9.463 0.056
## i 171.277 6.133 27.929 0.000 1.000 1.000
## s 30.953 22.137 1.398 0.162 1.000 1.000
##
## R-Square:
## Estimate
## CCt1_p1 0.914
## CCt2_p1 0.901
## CCt3_p1 0.862
## CCt4_p1 0.886
## CCt5_p1 0.944semPaths(fit_CCm1)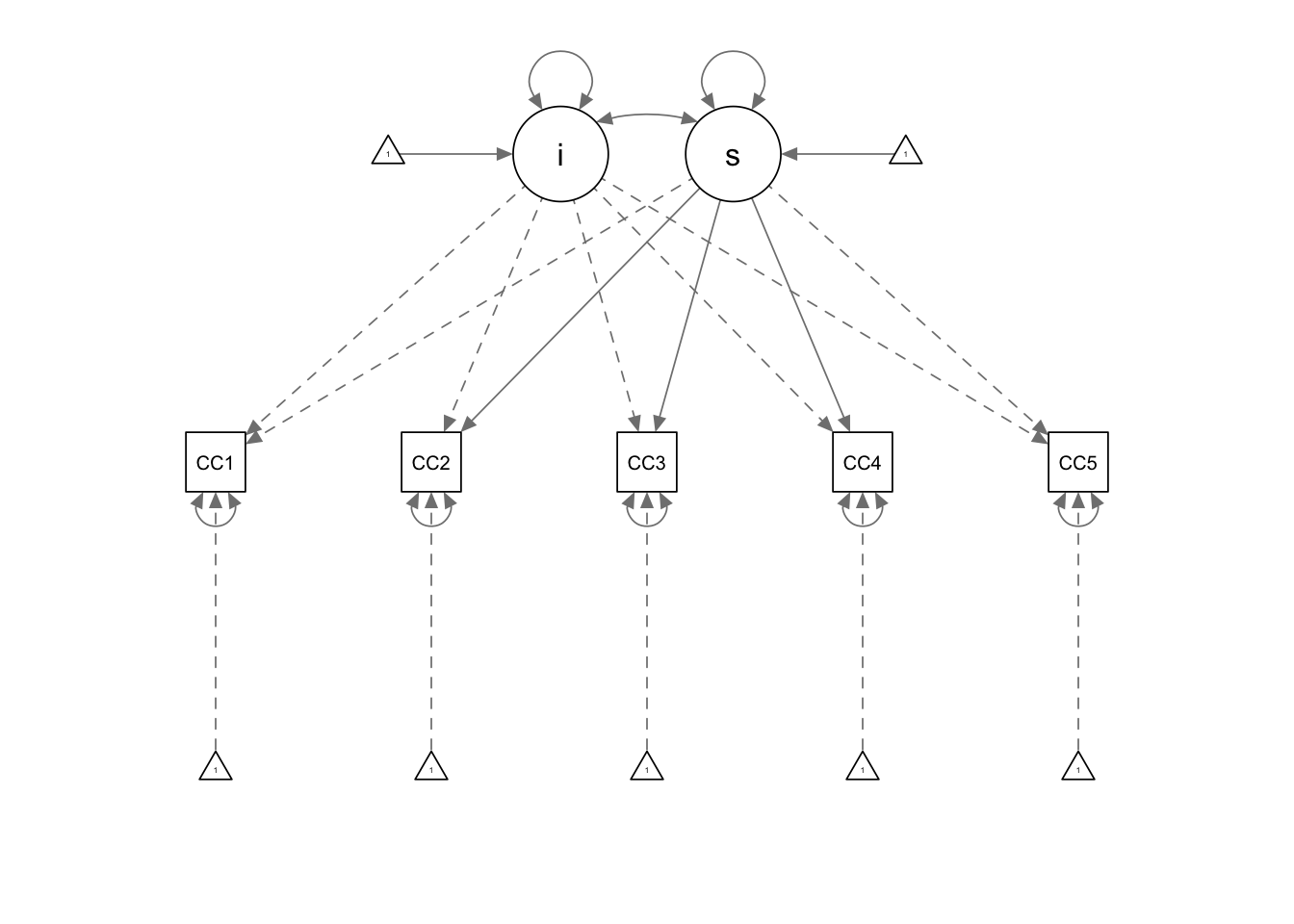
Fornix
Interpreting the results - Fornix
It was not possible to fit a latent basis growth model and, therefore, a latent growth model has been fitted.
Chi-square test of overall model fit:
- The chi-square test (chisq = 13.690, p= 0.188), was not statistically significant, therefore, no indication of poor model fit.
Comparative Fit Index (CFI):
- values is above 0.95 (CFI = 0.999),therefore, indicate good model fit.
Root mean square error of approximation (RMSEA):
- Value is less than 0.05 (RMSEA = 0.006), therefore, indicating a good model fit.
Interpreting the model
Variances:
Intercept (118.869, p=0.000)
Slope (0.486, p =0.756)
Intercepts i:
- Mean for the latent intercept, i, is 49.551, indicating that on average the DTI strength is around 50 at all time periods.
Intercepts s:
- Mean for the latent slope, s, is 0.102, indicating that on average DTI increased less than 0.1 units between each time point.
Covariance:
- The covariance between the intercept and slope,-3.832, suggests that there is less DTI growth for those participants that had higher DTI scores at time point one than for those participants with lower DTI.
Residual variances (unexplained variance):
- The residual variances are between 27-32, indicating that each single-latent intercept model explained 68-73% of the variability in DTI scores.
Fom1 <- '
i =~ 1*Fot1_p1 + 1*Fot2_p1 + 1*Fot3_p1 + 1*Fot4_p1 + 1*Fot5_p1
s =~ 0*Fot1_p1 + 1*Fot2_p1 + 2*Fot3_p1 + 3*Fot4_p1 + 4*Fot5_p1
'
fit_Fom1 <- growth(Fom1, data=FoPOMPSGMMDTI, missing="fiml",estimator='mlr',bounds="pos.lv.var", em.h1.iter.max= 10000)
fitMeasures(fit_Fom1,fit.measures=c("dfi","chisq","cfi","rmsea","srmr")) ## chisq cfi rmsea srmr
## 13.690 0.999 0.006 0.040summary(fit_Fom1, standardized=T, rsquare=T)## lavaan 0.6.16 ended normally after 131 iterations
##
## Estimator ML
## Optimization method NLMINB
## Number of model parameters 10
##
## Number of observations 10808
## Number of missing patterns 13
##
## Model Test User Model:
## Standard Scaled
## Test Statistic 13.690 12.125
## Degrees of freedom 10 10
## P-value (Chi-square) 0.188 0.277
## Scaling correction factor 1.129
## Yuan-Bentler correction (Mplus variant)
##
## Parameter Estimates:
##
## Standard errors Sandwich
## Information bread Observed
## Observed information based on Hessian
##
## Latent Variables:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## i =~
## Fot1_p1 1.000 10.903 0.896
## Fot2_p1 1.000 10.903 0.924
## Fot3_p1 1.000 10.903 0.940
## Fot4_p1 1.000 10.903 0.951
## Fot5_p1 1.000 10.903 0.962
## s =~
## Fot1_p1 0.000 0.000 0.000
## Fot2_p1 1.000 0.697 0.059
## Fot3_p1 2.000 1.394 0.120
## Fot4_p1 3.000 2.091 0.182
## Fot5_p1 4.000 2.788 0.246
##
## Covariances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## i ~~
## s -3.832 3.120 -1.228 0.219 -0.504 -0.504
##
## Intercepts:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## .Fot1_p1 0.000 0.000 0.000
## .Fot2_p1 0.000 0.000 0.000
## .Fot3_p1 0.000 0.000 0.000
## .Fot4_p1 0.000 0.000 0.000
## .Fot5_p1 0.000 0.000 0.000
## i 49.551 0.128 387.687 0.000 4.545 4.545
## s 0.102 0.045 2.245 0.025 0.146 0.146
##
## Variances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## .Fot1_p1 29.111 6.905 4.216 0.000 29.111 0.197
## .Fot2_p1 27.549 3.717 7.412 0.000 27.549 0.198
## .Fot3_p1 28.933 2.355 12.286 0.000 28.933 0.215
## .Fot4_p1 31.189 4.574 6.819 0.000 31.189 0.237
## .Fot5_p1 32.404 9.319 3.477 0.001 32.404 0.252
## i 118.869 7.505 15.839 0.000 1.000 1.000
## s 0.486 1.567 0.310 0.756 1.000 1.000
##
## R-Square:
## Estimate
## Fot1_p1 0.803
## Fot2_p1 0.802
## Fot3_p1 0.785
## Fot4_p1 0.763
## Fot5_p1 0.748semPaths(fit_Fom1)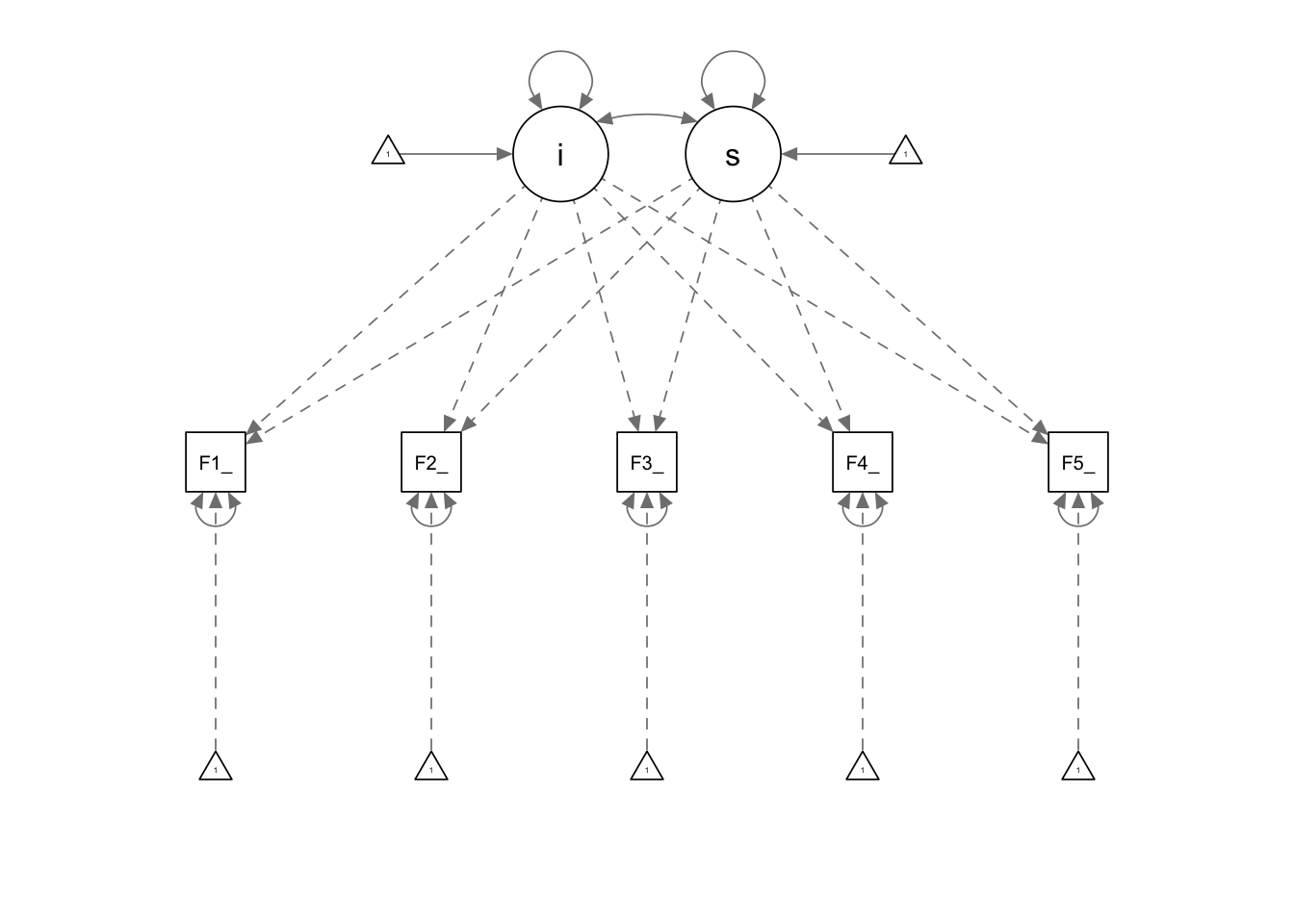
Anterior Thalamic Radiations
Interpreting the results - Anterior Thalamic Radiations
Chi-square test of overall model fit:
- The chi-square test (chisq = 7.938, p= 0.338), was not statistically significant, therefore, no indication of poor model fit.
Comparative Fit Index (CFI):
- Value is above 0.95 (CFI = 1),therefore, indicating a good model fit.
Root mean square error of approximation (RMSEA):
- Value is less than 0.05 (RMSEA = 0.004), therefore, indicating a good model fit.
Interpreting the model
Variances:
Intercept (95.826, p=0.000)
Slope (18.098, p =0.756)
Intercepts i:
- Mean for the latent intercept, i, is 49.969, indicating that on average the Fornix DTI strength is around 50 at all time periods.
Intercepts s:
- Mean for the latent slope, s, is 3.105, indicating that on average DTI increased around 3 units between each time point.
Covariance:
- The covariance between the intercept and slope, -26.763, suggests that there is less DTI growth for those participants that had higher DTI scores at time point one than for those participants with lower DTI.
Residual variances (unexplained variance):
- The residual variances are between 23-29, indicating that each single-latent intercept model explained 71-77% of the variability in DTI scores.
Atrm1 <- '
i =~ 1*Atr1_p1 + 1*Atr2_p1 + 1*Atr3_p1 + 1*Atr4_p1 +1*Atr5_p1
s =~ 0*Atr1_p1 + Atr2_p1 + Atr3_p1 + Atr4_p1 + 1*Atr5_p1
'
fit_Atrm1 <- growth(Atrm1, data=AtrPOMPSGMMDTI, missing="fiml",estimator='mlr',em.h1.iter.max= 10000)
fitMeasures(fit_Atrm1,fit.measures=c("dfi","chisq","cfi","rmsea","srmr")) ## chisq cfi rmsea srmr
## 7.938 1.000 0.004 0.039summary(fit_Atrm1, standardized=T, rsquare=T)## lavaan 0.6.16 ended normally after 237 iterations
##
## Estimator ML
## Optimization method NLMINB
## Number of model parameters 13
##
## Number of observations 10808
## Number of missing patterns 13
##
## Model Test User Model:
## Standard Scaled
## Test Statistic 7.938 5.562
## Degrees of freedom 7 7
## P-value (Chi-square) 0.338 0.592
## Scaling correction factor 1.427
## Yuan-Bentler correction (Mplus variant)
##
## Parameter Estimates:
##
## Standard errors Sandwich
## Information bread Observed
## Observed information based on Hessian
##
## Latent Variables:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## i =~
## Atr1_p1 1.000 9.789 0.895
## Atr2_p1 1.000 9.789 0.940
## Atr3_p1 1.000 9.789 0.968
## Atr4_p1 1.000 9.789 1.017
## Atr5_p1 1.000 9.789 1.083
## s =~
## Atr1_p1 0.000 0.000 0.000
## Atr2_p1 0.368 0.068 5.431 0.000 1.564 0.150
## Atr3_p1 0.464 0.073 6.397 0.000 1.975 0.195
## Atr4_p1 0.706 0.071 9.960 0.000 3.004 0.312
## Atr5_p1 1.000 4.254 0.471
##
## Covariances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## i ~~
## s -26.763 28.446 -0.941 0.347 -0.643 -0.643
##
## Intercepts:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## .Atr1_p1 0.000 0.000 0.000
## .Atr2_p1 0.000 0.000 0.000
## .Atr3_p1 0.000 0.000 0.000
## .Atr4_p1 0.000 0.000 0.000
## .Atr5_p1 0.000 0.000 0.000
## i 49.969 0.161 310.870 0.000 5.105 5.105
## s 3.105 0.337 9.226 0.000 0.730 0.730
##
## Variances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## .Atr1_p1 23.925 15.009 1.594 0.111 23.925 0.200
## .Atr2_p1 29.902 4.033 7.415 0.000 29.902 0.276
## .Atr3_p1 27.378 2.878 9.514 0.000 27.378 0.268
## .Atr4_p1 25.565 5.450 4.690 0.000 25.565 0.276
## .Atr5_p1 21.239 18.134 1.171 0.242 21.239 0.260
## i 95.826 15.032 6.375 0.000 1.000 1.000
## s 18.098 58.270 0.311 0.756 1.000 1.000
##
## R-Square:
## Estimate
## Atr1_p1 0.800
## Atr2_p1 0.724
## Atr3_p1 0.732
## Atr4_p1 0.724
## Atr5_p1 0.740semPaths(fit_Atrm1)
Ayla Pollmann - 2023